信封、桥梁、鸟类和鱼类 | 科学游戏

我们上周的杂耍演员在过这样一座危险的桥时,没有做出最好的决定,他把木桩抛向空中,因为他在垂直向上抛木桩时产生的反作用力——以及木桩回到马戏团演员手中时产生的冲击力——对桥施加的力大于桥的静止重量。即使是杂耍演员也无法绕过牛顿第三定律。 有些读者建议使用秤来检查上述情况并量化效果。如果您家里有一台典型的“称重机”来监测饮食效果(并且天花板足够高),您可以自行承担风险尝试以下实验:拿一个重一公斤或以上的物体(例如一盒任何液体),站在秤上,双手握住它,将其稍微向上抛出,同时不要忽略秤的标记;您会看到在抛出和取回物体的那一刻(如果您设法在飞行中将其取回),指针会稍微向右移动。 更多信息 玩杂耍的人的问题让人想起许多年前在一所工程学院的物理考试中提出的一个问题,当时它变得很有名: 秤上有一个笼子,空笼子重 1 公斤,笼子摇杆上栖息着一只重 30 克的小鸟。突然,小鸟开始在笼子里飞来飞去。秤上的指针显示多高? 同一主题的变体: 现在是一个小鱼缸,里面有一条鱼,鱼在秤上。鱼缸和水重一公斤,鱼重30克。突然,鱼跳出水面,又落回鱼缸里。这次跳跃对秤针有什么影响? 还有一个变化: 上图的鱼缸里,水量一样,但缸底没有鱼,而是一颗重一公斤的铁球。如果你把手伸进鱼缸,拿出铁球,在这个动作的不同时刻,秤上的指针指向什么? 信封和桥梁的等价性 从一个关于桥梁的问题(介词的两个含义)到另一个关于信封和平行桥的问题: 著名的 柯尼斯堡的 7 座桥梁 这是不可能的,因为城市的四个部分都有奇数座桥:其中一个岛屿有 5 座,另一个岛屿有 3 座,河的右岸有 3 座,左岸有 3 座(总共 14 座,是的,但每座桥我们都数了两次)。因此,无论从哪里开始,如果您过完所有桥而不再经过任何一座,那么您必须做一些不可能的事情才能完成任务:同时完成其他三个部分的路线(因为您将按照进入-退出-进入的顺序访问所有部分,或者在有 5 座桥的岛屿上按照进入-退出-进入-退出-进入的顺序访问所有部分)。要使欧拉路线从一个区域开始并在另一个区域结束(就像今天的加里宁格勒一样),必须有两个区域的桥梁数量为偶数,两个区域的桥梁数量为奇数。 从柯尼斯堡到加里宁格勒,从 7 座桥到 5 座桥,有 21 对不同的桥可能消失(7×6/2)。其中 15 对消失后,会留下两个区域,其中桥数为偶数,另两个区域为奇数。例如,如果我们消除图中标记的桥(乍一看似乎是最可有可无的),两个岛屿都剩下 3 座桥,两岸都剩下 2 座桥。因此,我们需要一些额外的数据来知道 15 对可能的桥中哪一对已被消除。我们可以肯定的是,无论消失的桥是什么,现在加里宁格勒桥的可解问题等同于众所周知的画一个打开的信封的问题,即不把铅笔从纸上抬起来或在同一条线上画两遍。你看到等价了吗?不要说加里宁格勒的区域是 4,而信封有 5 个顶点(你为什么不这么说?)。 由于我们已经讨论了几个星期的图表,尽管几乎没有提到它们的名字,我借此机会再次推荐克拉拉·格里马 (Clara Grima) 的精彩有趣的书 寻找丢失的图表就像我在她生日那天说的那样,当我开始阅读它时,我想:“我为什么不写它?”但是当我读完它时,我对自己说:“她写它更好。” […]
有问题的桥梁 | 科学游戏

上周提出的摇摇欲坠的梯子问题是经典谜语的一个变体,在经典谜语中,你必须满足某些要求(比如著名的牧羊人带着狼、羊和卷心菜过河的谜语),只是河流被梯子代替,船被灯笼代替,并增加了速度因素。这让我们提出了以下元问题:从河流的角度来看,楼梯问题会是什么样子?换句话说:你能想出一个等效的方法,用河流和船代替梯子和灯笼吗?这不是提出类似的问题,而是提出一个严格等效的问题。David Fernández 给出的梯子问题解决方案可以促进“变量变化”: “手电筒问题的理想情况是,两个最慢的人一起下去,节省 4 分钟,而且他们两个都不必上去递手电筒(否则,我们什么也省不了)。要做到这一点,两个最快的人必须先下去。顺序是:两个最快的人下去,2 分钟,其中一个人上去把手电筒交给两个最慢的人,8 分钟,另一个最快的人上去,两个最快的人再下去,2 分钟:12 分钟的下行时间加上 3 分钟的上行时间,一共 15 分钟。” 更多信息 软木塞的改进也引发了许多有趣的评论。最实用的解决方案是杂志上发表的解决方案 大众机械,具体方法是通过几个垂直切口(用非常锋利的刀,这样软木塞就不会碎裂)从软木塞上取下一个圆柱形(或截锥形)部分,如图所示。通过取出楔子并用手指挤压软木塞以连接切口的内表面,塞子的直径会略微减小。 另一种不太实用但从理论角度来看很有趣的解决方案是将软木浸入水下几米(仅 10 米深度的压力就已达到 2 个大气压)以压缩软木。有趣的是,软木的压缩性非常好,即使浸入水中很深,它也不会浮出水面,因为它的密度等于周围水的密度,因此不会漂浮。 位置的几何和物理 梯子和灯笼的问题是对“桥梁和火炬之谜”的建筑改编(原谅阿根廷主义)(该谜题定期在网上传播, 有自己的维基百科条目),这是解决其他桥梁问题的好借口。 最著名的当然是柯尼斯堡七座桥梁,欧拉的巧妙解决可以说开创了图论。顺便说一句,这也极大地推动了后来被称为拓扑学的学科的发展,即研究几何物体的结构特性,这些特性与其具体尺寸和形状无关(欧拉本人称之为 geometria situs,即位置几何)。顺便说一句,加里宁格勒(旧柯尼斯堡的新名称)目前只有五座桥梁,现在可以从一个岛开始旅程,在另一个岛上结束旅程,尽管无法完成欧拉循环,即在同一点开始和结束路线。有了这些数据,你能在加里宁格勒地图上标出目前的五座桥梁吗? 从几何到位置的物理学,特别是玩杂耍的人在一座不安全的桥上的有问题的位置: 一个玩杂耍的人正准备过一座非常脆弱的桥,这座桥最多只能承受 50 公斤的重量。玩杂耍的人个子很小,只有 48 公斤重,但他的三个杂耍柱子每个重 1 公斤。“没问题,”玩杂耍的人想,“我会把柱子抛向空中,这样空中至少会有一根柱子,而且这座桥承受的重量不会超过 50 公斤。”你认为这是个好主意吗?你能想出其他解决方案吗? 我邀请我的睿智读者(除非他们患有桥梁恐惧症)去寻找和提出其他桥梁问题,据我所知,这个话题很少被利用,尽管从原则上讲,它可以在逻辑数学和物理层面上发挥很大的作用。 您可以关注 魔装 在 Facebook, X 埃 Instagram或在此注册以接收 我们的每周新闻通讯。 1719157294 #有问题的桥梁 #科学游戏 2024-06-21 07:42:15
数学:奇怪的巧合 | 科学游戏

上周,有人在谈论著名的克里特岛迷宫时提出了一个问题:迷宫是无法逃脱的,这是一个矛盾。 在方面:根据定义,迷宫必须至少有一个可行的入口和出口(可以相同);否则它就不是迷宫,而是监狱。 至于博尔赫斯提到的所谓迷宫,即人们总是向左转才能离开,人们认为这位阿根廷作家对数学很着迷,但对数学却不太了解,因此他把最简单的方法(尽管并不总是最快的方法)与离开相关迷宫的方法混淆了,即用左手触摸墙壁,然后向前移动,朝一个方向或另一个方向,中间不要停下触摸墙壁。显然,用一只手还是另一只手并不重要,除非你是右撇子,用右手握着剑来面对牛头怪。要使这种方法奏效,迷宫必须连接起来,也就是说,所有部分必须连接在一起形成一个整体。如果是独立的块,一个在另一个里面,事情就会变得复杂;但无论迷宫有多大、多复杂,总有相对简单的方法可以离开它。 更多信息 不太可能发生的事情很可能会发生 而且无论事件发生的概率有多小,它都有可能发生(否则它就不是不可能发生的,而是不可能发生的)。而且由于很多事情总是在发生,所以非常不可能发生的事情很可能会发生,正如亚里士多德在他的《论自然》中指出的那样。 诗论。 上周我们问自己,同一天出现两篇标题相似的文章的可能性有多大 博尔赫斯解构 是 博尔赫斯被拆解尽管没有人计算过它(我的意思是使用“费米”近似,因为考虑到无数的因素,精确的计算是不可行的),但这是一个很好的借口来谈论一些令人惊叹的巧合,经过简单的分析后,这些巧合就不再存在了。 当然,也有一些真正非凡的巧合,其中最引人注目的一个就是从地球上看,太阳和月亮具有相同的视大小,这使得日食的奇妙景象成为可能。但在许多其他令人惊叹的巧合中,令人惊讶的是与我们对现实的理解中的微妙的心理偏见有关。 一些并非不可能发生的事情看起来极不可能,最常见的原因之一是,我们头脑中个人和群体的考虑往往会重叠。在一群人中,其中一个人的生日和你同一天的概率非常低:1/365(事实上,还要小一点,因为必须考虑闰年:你能成为一个纯粹主义者并计算出准确的概率吗?);但是,在一个不是很大的群体中,有两个人在同一天过生日的概率相当高:从 23 个人来看,这个概率超过了 50%(你能计算出 23 个人的准确概率吗?)。 即使是在小群体中,巧合的发生率也会高于直觉所预测的巧合。在一个 7 人群体中,您认为其中两人生日在同一周的概率是多少?两人属于同一星座的概率是多少?顺便说一句,有必要澄清一下“同一周”的含义(我留给您自行判断)。 无需与任何人见面,你只需用一副简单的纸牌就能测试一些看似不可能发生的事件的发生概率。如果你把纸牌放在桌子上,并按顺序说出它们的名字(“五角星 A、五角星二、五角星三……圣杯 A、圣杯二、圣杯三……”),在说出某张特定纸牌(例如梅花侍从)时出现的概率是 1/40;但任何纸牌“神奇地”匹配其召唤的概率都相当高(你能计算出来吗?)。高到你可以用双倍赌注对单倍赌注下注,以保证它会发生。 您可以关注 魔装 在 Facebook, X 埃 Instagram点击此处接收 我们的每周新闻通讯。 1716553242 #数学奇怪的巧合 #科学游戏 2024-05-24 08:46:51
博尔赫斯与无限| 科学游戏

豪尔赫·路易斯·博尔赫斯对巴别塔图书馆的艺术再现。国会图书馆 通过折叠上周的 2×3 地图,不可能根据纳博科夫字谜 OSBERG 重建博尔赫斯。 只要认识到“BORGES”这个词中的“E”和“S”在一起,在“OSBERG”网格中占据的方格只共享一个顶点,任何折叠都不可能使两个方格“与顶点相对”相邻,这一点就足够了。 因此,我们也不能从 BORGES 转到 OSBERG:在这种情况下,在顶点对面的框中有两对字母(BE 和 OS),在 OSBERG 中它们在一起。 关于折叠三联画、多联画和基本地图的不同可能性,我们的定期评论员弗朗西斯科·蒙特西诺斯(Francisco Montesinos)进行了非常详细的分析(见上周的评论),由于篇幅原因,我无法完整复制; 这就是他关于 2×2 元素图的说法(顺便说一句,在括号中,他暗示了我们刚刚看到的不可能性): “在 2×2 的情况下,从左到右、从上到下对纸张(1、4、2、3)进行编号,有 24 种排列,其中 8 种给出了不可能的配置(对角位置的两页将有一些交错) )并且在剩余的 16 个中,8 个将是对称的,因此将有 8 种不同的可能折叠。 达到相同结果的另一种方法是考虑如果第一张纸固定在前视图中(4 种可能性),则对于下一张纸,只有 2 种可能性,而对于其余两个位置只有一种可能性,总共 8 种。 更多信息 博尔赫斯拆解 上一篇文章发表后 科学游戏, 博尔赫斯解构一篇文章标题为 博尔赫斯拆解,很难相信,仅仅相隔几个小时,两篇标题如此相似的文本纯粹是偶然发表的。 (我邀请精明的读者计算“费米方式”,即此类事件随机发生的概率的数量级)。 无论如何,上述文章除其他外指出:“博尔赫斯将无限的概念置于其作品的中心,这一概念在他的叙述和散文中都发挥着至关重要的作用。 书中的书籍无穷无尽 巴别塔图书馆永恒反射的镜子 特隆、乌克巴尔、第三世界无尽的迷宫只是博尔赫斯如何挑战我们对时间和空间的理解,引导我们质疑现实本身的几个例子。” 在现实(本身)中,所提到的三件事都不是无限的:可能的书籍数量——尽管巨大——是有限的,甚至很容易计算,正如德国数学家和哲学家库尔德·拉斯维兹(Kurd Lasstwiz,1848-1910)已经在他的开创性故事 通用图书馆博尔赫斯受到启发而写作 巴别塔图书馆。 而相互反射的镜子的反射速度如此之慢——从天文学的角度来看,光速微乎其微——以至于它们在宇宙灭绝之前所能产生的图像数量不仅不是无限的,而且不是无限的。与其他数字怪物(例如可能的国际象棋游戏)相比,甚至非常大。 […]
博尔赫斯解构 | 科学游戏

弗拉基米尔·纳博科夫饰演豪尔赫·路易斯·博尔赫斯。托尼·阿姆斯特朗·琼斯 三联画,即一张风景纸被两个垂直折叠分成三等份,原则上可以像我们上周看到的那样,以 8 种不同的方式折叠:在每种折叠中,我们可以覆盖纸张的正面或背面,所以有 4 种可能性(AA、AR、RA、RR)从一种折叠开始,从另一种折叠开始有 4 种,总共 8 种; 但只是在原则上,因为其中两个折叠产生与另外两个折叠相同的配置(你能确定它们是哪一个吗?),所以实际上只有 6 种不同的折叠。 如果你不喜欢心理想象,我建议你折叠一张纸来制作三联画,并将边从1到6编号(或者更好的是正面为A1、A2、A3,背面为R1、R2、R3) )您将能够花一段既有趣又富有启发性的时间来研究不同的折叠可能性。 类似地,“四联画”(一张横向纸被三个垂直折叠分成四个相等的部分)的可能的不同折叠不是 24(从 3 个折叠中的每一个开始,2 x 2 x 2 = 8 种可能性:3 x 8 = 24 ),但只有 16 个。如果三联画看起来太简单,请尝试找到“四联画”的 16 个不同折叠(或者相当于同一事物,确定哪些是重复的)。 更多信息 印章条问题 折叠“多联画”(即只有垂直折叠的横向纸张)看似简单的问题通常被称为“邮票条问题”,其中这是一个执行完整折叠的问题,即放置它们的问题所有这些都在其中一个下面,形成紧凑的一堆。 在 0 次和 1 次折叠的简单情况下,分别有 1 种和 2 种不同的配置,并且正如我们所见,2 次和 3 次折叠分别有 6 种和 16 种可能性。 该序列继续快速增长: […]
折叠地图的艺术| 科学游戏

像纸飞机一样折叠的地图。阿拉米库存照片 如果我们将 DIN A0 板材(DIN 系列的起源)的边数逐一相乘,如我们上周所见,我们将得到: 841 毫米 x 1189 毫米 = 1000049 平方毫米 也就是说,正如欧文·肖尔 (Erwin Schorr) 在评论中指出的那样,几乎正好是一平方米,误差仅为万分之五十。 关于通过折叠纸到达月球的可能性,萨尔瓦·富斯特评论如下: “纸张的厚度约为十分之一毫米,将其折叠 10 次后,我们将得到初始厚度的 210 倍,这意味着比初始厚度大约增加 1,000 倍,即 100 毫米(0.1 m)厚的。 。 现在,每折叠10次,厚度就会增加1000倍。 因此,如果我们从初始情况进行 40 次折叠,我们将得到: 0.1 mm – 100 mm – 100 m – 100 km – 100,000 km 如果再进行几次折叠,我们就已经超过了到月球的距离,因为通过进行两次折叠,我们已经超过了到月球的距离。更多折叠,我们会将前面的最后一个值乘以 4。总之,42 折叠就足够了。 关于纸张的尺寸,考虑到A4纸最多可折叠7次,A3可折叠8次,A2可折叠9次,A1可折叠10次,A0可折叠11次,即1平方米的纸张。 它可以折叠11次。 如果我们想要达到42倍,我们就必须将其翻倍31倍,这意味着将表面积增加到2立方米,即大约20亿平方米,或者换句话说,大约2000平方公里,类似的大小从 吉普斯夸 […]
折纸艺术| 科学游戏
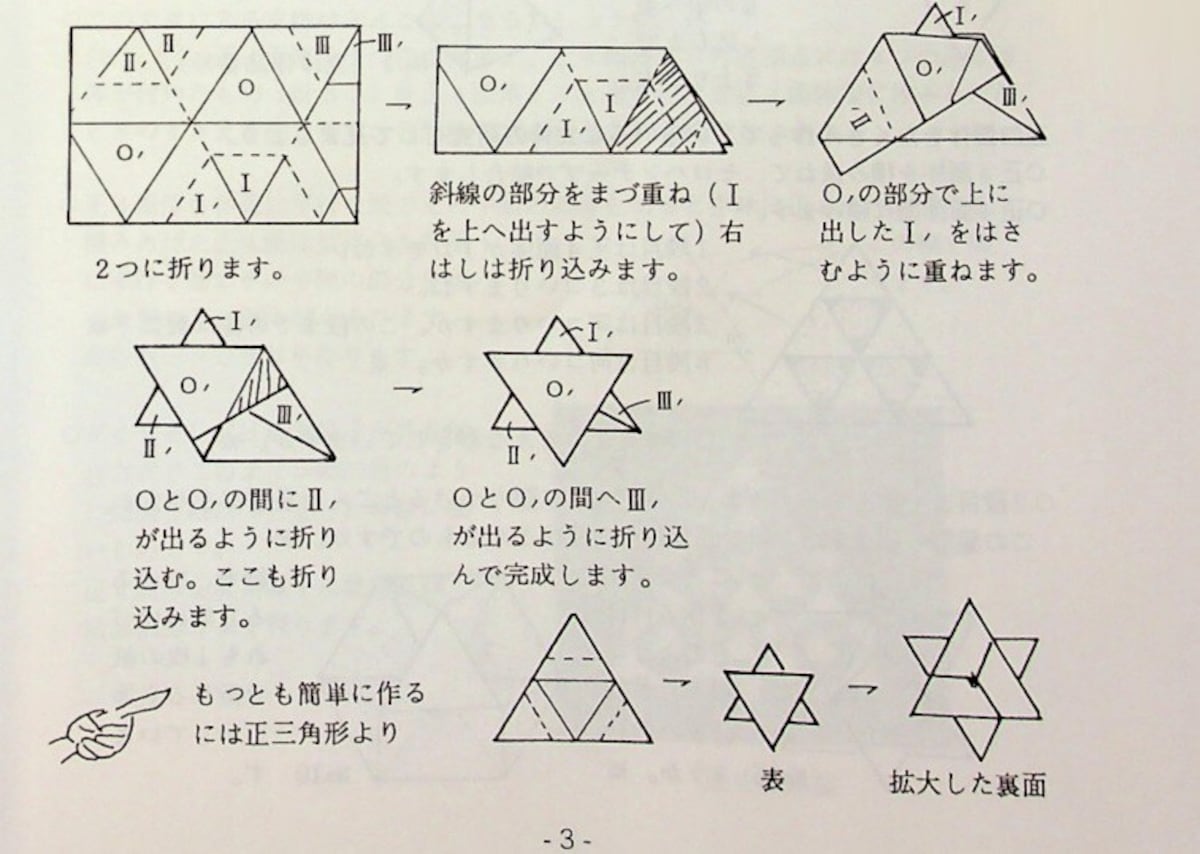
黄金矩形和上周提到的熟悉的 DIN A4 纸都具有易于自我复制的特性。 如果我们从黄金矩形中删除一个边长等于其较小边的正方形,则剩下的矩形与第一个矩形类似(因此也是黄金矩形)。 如果我们以初始矩形的短边为单位,将其长边称为x,为了使两个矩形相似,它们的边必须成比例,因此: x:1 = 1:(x-1) x2 – x – 1 = 0 x = 1.618… = Φ(黄金数) 更多信息 对于 DIN A4 纸张,自我复制更加简单:将其对折,我们得到两张与整张纸类似的 DIN A5 纸张。 如果我们再次以纸张的短边为单位并将长边称为 x,我们现在将得到: x:1 = 1:(x/2) x²/2 = 1 x = √2 = 1,414… DIN A4 这个名字来自于 德国标准化研究所:DIN 是 Deutsches Institut für Normung 的缩写,4 表示原始纸张 A0(尺寸为 841×1189 […]
神圣的多边形和被诅咒的星星| 科学游戏

正如我们上周所看到的,半径为 1、2 和 3 且彼此相切的圆心是直角三角形的顶点。 而且不只是任何一个,而是边长为 3、4 和 5 的那个,正是埃及人的神圣三角形,他们知道与这个三角形的最长边相对的角度是正确的,尽管不确定他们是否概括了这一点这个结果适用于所有边满足关系 a² = b² + c² 的三角形(即,他们知道毕达哥拉斯定理)。 正如 Salva Fuster 指出的那样:“对于半径分别为 1、2 和 3 的彼此相切的圆,一旦将它们的圆心画成边长为 3、4 和 5 的直角三角形,就很容易看出,这三个圆的外切圆将为 6,并且其圆心将恰好位于与其他三个圆心形成矩形的点处。” (因为?)。 更多信息 用几何方法求内切圆的半径并不是那么简单。 我们可以借助公式: Q² + R² + S² + T² = 1/2 (Q + R+ S + T)² 但是,正如我们所见,计算又长又麻烦,因此使用另一个直接给出 T 的公式会很方便: T = Q + […]
当在空中抛硬币时,它更有可能落在抛掷的同一面 | 咖啡和定理| 科学
想象一下,您拿起一枚硬币,准备将其扔到空中。 你认为它正面朝上的概率是多少? 从哪一边扔出去有关系吗? 大多数人都会说 出现正面的概率是 50%不管硬币的初始位置如何,但事情并没有那么简单。 前两个问题对应于两个不同的事件。 第一个涉及正面或反面出现的概率,两者都是一样的。 然而,第二个指的是如果硬币在抛出之前面朝上,则正面朝上的概率。 第二个概率称为条件概率,可以与第一个概率不同。 关于这个问题,2007年,数学家 佩里斯·迪肯, 苏珊·霍姆斯 理查德·蒙哥马利(Richard Montgomery)提出了一个物理模型,该模型显示出轻微的偏向于硬币在抛掷时落地的情况。 总之,他们指出,当向空中抛掷硬币时,51% 的情况下硬币会落在抛掷的同一面。 然而,如果您不知道硬币是如何放置的,则正面或反面出现的概率为 50%。 但怎么可能完全确定地说概率就是这样呢? 这是一个估计问题,也就是说,从一开始我们就不知道获得正面的概率,我们想根据证据正确估计它的值。 更多信息 使其成为解释的一部分的最著名的方法 作为频率的概率,从而产生了所谓的频率统计。 更具体地说,在这种方法下,我们想要估计的概率被解释为在相同条件下无限多次抛硬币时观察到的正面的比例。 因此,为了近似它,在相同条件下多次抛硬币就足够了,并通过观察到的正面的比例来近似真实概率。 概率论和统计学史上的伟大人物都使用了频率论方法,例如 布冯伯爵 哦 卡尔·皮尔逊。 首先,他抛硬币 4040 次,得到 2048 个正面,这代表概率估计为 4040/2048 = 0.5069,即 50.69%; 第二个投掷了 24,000 次,其中 12,012 次摔倒,露出脸部的概率为 50.005%。 然而,这种方法的出发点造成了一定的悖论:在完全相同的条件下抛硬币,难道不会得到相同的结果吗? 牛顿物理学 我肯定是的,事实上,正是最初的微小变化导致了结果的随机性,这就是为什么考虑重复的前提是自相矛盾的。 当研究患病概率时,这个起点就更加难以捉摸……那么,应该重复什么呢? 人的一生? 另外,需要抛多少次才能足够接近真实值? 因此,尽管频率论方法是一种有效且经过充分研究的方法,但它有时会导致某些难以解释的推理,甚至导致它在一些科学期刊中受到质疑。 更多信息 为了克服这些限制,可以使用另一种统计方法: 什么是所谓的贝叶斯。 […]
施泰纳椭圆 | 科学游戏
正如我们所看到的 上星期,“女学生问题”承认 7 个非同构解(即具有不同的结构),由美国数学家 Frank Nelson Cole(1861-1926)于 1922 年列出,他在 20 世纪初因发现第 67 个梅森数 (2⁶⁷– 1) 的因子。 爱德华·卢卡斯(Édouard Lucas)已经证明 M₆₇ 不是素数,但他无法分解它。 当纸和笔是唯一可用的计算器时,科尔完成了找到这些因素的壮举(正如他承认的那样,三年来每周日都致力于解决这个问题): M⁶⁷ = 147.573.952.589.676.412.927 = 193.707.721 × 761.838.257.287 科尔还计算了(与之前的计算相比有点小)女学生问题的解总数 – 包括同构解: 十五! x 13/42 = 404,756,352,000(你如何得到这个数字?)。 更多信息 正椭圆和椭圆 正如我们上周看到的,瑞士数学家雅各布·施泰纳(Jakob Steiner)除了对组合设计理论做出了重要贡献(他的“最小树”——图形盆景—— 我们已经处理这个问题五年了)是有史以来最伟大的几何学家之一; 据一些人说,他是佩尔加的阿波罗尼乌斯之后最伟大的人物。 他厌恶解析几何,认为解析几何污染了“纯”几何,他的工作完全基于合成和射影几何的方法,他对合成和射影几何的发展做出了显着的贡献。 在谈论施泰纳时提到阿波罗尼乌斯特别相关,因为像这位伟大的几何学家一样,他对几何学做出了重要贡献。 二次曲线的研究。 在这一领域,斯坦纳最著名的是他的三角形外接椭圆和内接椭圆。 施泰纳外接椭圆是唯一通过一个椭圆的所有三个顶点的椭圆 三角形 其中心是它的质心或质心(请记住,三角形的质心是其中线的交点,如果我们将其视为物理对象,则它与其重心重合)。 有人可能认为圆也是椭圆,因此三角形的外接圆也是斯坦纳外接椭圆。 但事实并非如此,因为外接圆的中心(外心)是三角形平分线的交点,而不是其中线的交点(原因很明显:三角形的所有点 媒体矩阵 每条边与该边对应的两个顶点的距离相等,因此平分线的交点与三个顶点的距离相等)。 在其他属性中,斯坦纳外接椭圆是所有由三角形外接的椭圆中面积最小的一个(你能根据三角形的面积计算它吗?)。 当我们在没有指定任何其他内容的情况下谈论斯坦纳椭圆时,我们指的是它的外接椭圆,不应将其与内椭圆混淆。 […]
