信封、桥梁、鸟类和鱼类 | 科学游戏

我们上周的杂耍演员在过这样一座危险的桥时，没有做出最好的决定，他把木桩抛向空中，因为他在垂直向上抛木桩时产生的反作用力——以及木桩回到马戏团演员手中时产生的冲击力——对桥施加的力大于桥的静止重量。即使是杂耍演员也无法绕过牛顿第三定律。

有些读者建议使用秤来检查上述情况并量化效果。如果您家里有一台典型的“称重机”来监测饮食效果（并且天花板足够高），您可以自行承担风险尝试以下实验：拿一个重一公斤或以上的物体（例如一盒任何液体），站在秤上，双手握住它，将其稍微向上抛出，同时不要忽略秤的标记；您会看到在抛出和取回物体的那一刻（如果您设法在飞行中将其取回），指针会稍微向右移动。

玩杂耍的人的问题让人想起许多年前在一所工程学院的物理考试中提出的一个问题，当时它变得很有名：

秤上有一个笼子，空笼子重 1 公斤，笼子摇杆上栖息着一只重 30 克的小鸟。突然，小鸟开始在笼子里飞来飞去。秤上的指针显示多高？

同一主题的变体：

现在是一个小鱼缸，里面有一条鱼，鱼在秤上。鱼缸和水重一公斤，鱼重30克。突然，鱼跳出水面，又落回鱼缸里。这次跳跃对秤针有什么影响？

还有一个变化：

上图的鱼缸里，水量一样，但缸底没有鱼，而是一颗重一公斤的铁球。如果你把手伸进鱼缸，拿出铁球，在这个动作的不同时刻，秤上的指针指向什么？

信封和桥梁的等价性

从一个关于桥梁的问题（介词的两个含义）到另一个关于信封和平行桥的问题：

著名的 柯尼斯堡的 7 座桥梁 这是不可能的，因为城市的四个部分都有奇数座桥：其中一个岛屿有 5 座，另一个岛屿有 3 座，河的右岸有 3 座，左岸有 3 座（总共 14 座，是的，但每座桥我们都数了两次）。因此，无论从哪里开始，如果您过完所有桥而不再经过任何一座，那么您必须做一些不可能的事情才能完成任务：同时完成其他三个部分的路线（因为您将按照进入-退出-进入的顺序访问所有部分，或者在有 5 座桥的岛屿上按照进入-退出-进入-退出-进入的顺序访问所有部分）。要使欧拉路线从一个区域开始并在另一个区域结束（就像今天的加里宁格勒一样），必须有两个区域的桥梁数量为偶数，两个区域的桥梁数量为奇数。

从柯尼斯堡到加里宁格勒，从 7 座桥到 5 座桥，有 21 对不同的桥可能消失（7×6/2）。其中 15 对消失后，会留下两个区域，其中桥数为偶数，另两个区域为奇数。例如，如果我们消除图中标记的桥（乍一看似乎是最可有可无的），两个岛屿都剩下 3 座桥，两岸都剩下 2 座桥。因此，我们需要一些额外的数据来知道 15 对可能的桥中哪一对已被消除。我们可以肯定的是，无论消失的桥是什么，现在加里宁格勒桥的可解问题等同于众所周知的画一个打开的信封的问题，即不把铅笔从纸上抬起来或在同一条线上画两遍。你看到等价了吗？不要说加里宁格勒的区域是 4，而信封有 5 个顶点（你为什么不这么说？）。

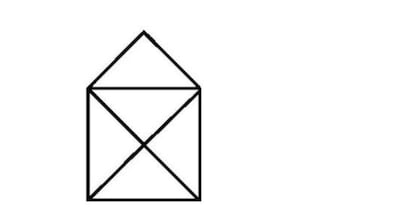
由于我们已经讨论了几个星期的图表，尽管几乎没有提到它们的名字，我借此机会再次推荐克拉拉·格里马 (Clara Grima) 的精彩有趣的书 寻找丢失的图表就像我在她生日那天说的那样，当我开始阅读它时，我想：“我为什么不写它？”但是当我读完它时，我对自己说：“她写它更好。”

您可以关注 魔装 在 Facebook， X 埃 Instagram或在此注册以接收 我们的每周新闻通讯。

_